Bits and Bit Fields

Bits and Bit Fields#

Some binary inputs use individual bits to specify contents. For instance, you might have a flag byte that holds multiple (bit) flags:

struct {
  unsigned int italic: 1;  // 1 bit
  unsigned int bold: 1;
  unsigned int underlined: 1;
  unsigned int strikethrough: 1;
  unsigned int brightness: 4;  // 4 bits
} format_flags;

How does one represent such bit fields in a Fandango spec?

Representing Bits#

In Fandango, bits can be represented in Fandango using the special values 0 (for a zero bit) and 1 (for a non-zero bit). Hence, you can define a <bit> value as

<bit> ::= 0 | 1

With this, the above format_flag byte would be specified as

<start>         ::= <format_flag>
<format_flag>   ::= <italic> <bold> <underlined> <strikethrough> <brightness>
<italic>        ::= <bit>
<bold>          ::= <bit>
<underlined>    ::= <bit>
<strikethrough> ::= <bit>
<brightness>    ::= <bit>{4}
<bit>           ::= 0 | 1

A <format_flag> symbol would thus always consist of these eight bits. We can use the special option --format=bits to view the output as a bit stream:

$ fandango fuzz --format=bits -f bits.fan -n 1 --start-symbol='<format_flag>'

00010001

Tip

The combination of --format=bits and --start-symbol is particularly useful to debug bit fields.

Internally, Fandango treats individual flags as integers, too. Hence, we can also apply constraints to the individual flags. For instance, we can profit from the fact that Python treats 0 as False and 1 as True:

$ fandango fuzz --format=bits -f bits.fan -n 10 -c '<italic> and <bold>'

01100111
10000101
11010111
01110111
11001000
01101110
01000101
10100001
00111010
00101100

Fandango strictly follows a “left-to-right” order - that is, the order in which bits and bytes are specified in the grammar, the most significant bit is stored first.

Hence, we can also easily set the value of the entire brightness field using a constraint:

$ fandango fuzz --format=bits -f bits.fan -n 1 -c '<brightness> == 0b1111'

10111111

Note

Fandango always strictly follows a “left-to-right” order - that is, the order in which bits and bytes are specified in the grammar.

Of course, we can also give the number in decimal format:

$ fandango fuzz --format=bits -f bits.fan -n 1 -c '<brightness> == 15'

00101111

01111111
11111111
11101111
10111111

10101111
01001111

00111111
00011111

01011111

Note how the last four bits (the <brightness> field) are always set to 1111 - the number 15.

Important

When implementing a format, be sure to follow its conventions regarding

  • bit ordering (most or least significant bit first)

  • byte ordering (most or least significant byte first)

Parsing Bits#

Fandango also supports parsing inputs with bits. This is what happens if we send a byte \xf0 (the upper four bits set) to the parser:

$ printf "\xf0" | fandango parse -f bits.fan -o - --format=bits

11110000

We see that the input was properly parsed and decomposed into individual bits.

This is the resulting parse tree:

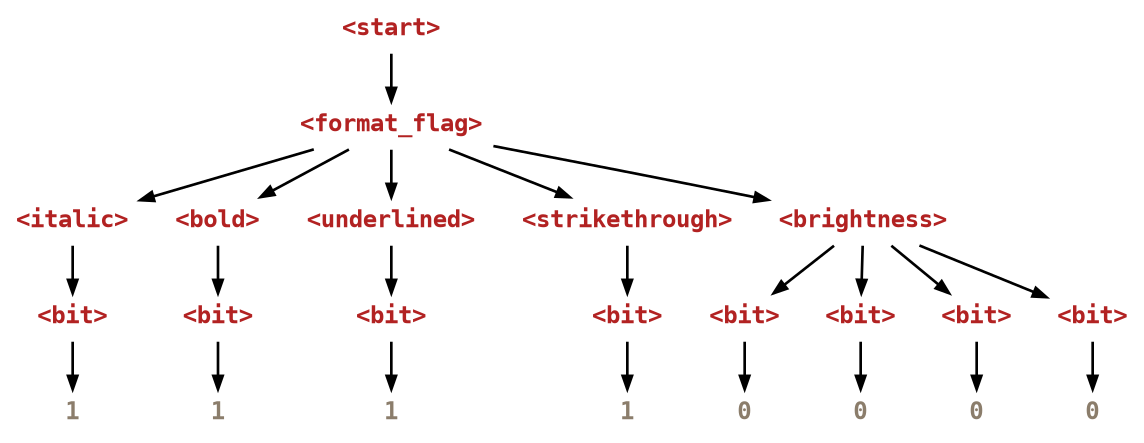
_images/d15b9d042456f2c1ffb1a08ef78a708e7fbbddc3393cb2069e814383d488bb8d.png

The grammar format shows us that the values are properly assigned:

$ printf '\xf0' | fandango parse -f bits.fan -o - --format=grammar

<start> ::= <format_flag>
  <format_flag> ::= <italic> <bold> <underlined> <strikethrough> <brightness>  # 0b11110000
    <italic> ::= <bit>
      <bit> ::= None + bits: 1  # Position 0x0000 (0), bit 7
    <bold> ::= <bit>
      <bit> ::= None + bits: 1  # Position 0x0000 (0), bit 6
    <underlined> ::= <bit>
      <bit> ::= None + bits: 1  # Position 0x0000 (0), bit 5
    <strikethrough> ::= <bit>
      <bit> ::= None + bits: 1  # Position 0x0000 (0), bit 4
    <brightness> ::= <bit> <bit> <bit> <bit>  # 0b0000
      <bit> ::= None + bits: 0  # Position 0x0000 (0), bit 3
      <bit> ::= None + bits: 0  # Position 0x0000 (0), bit 2
      <bit> ::= None + bits: 0  # Position 0x0000 (0), bit 1
      <bit> ::= None + bits: 0  # Position 0x0000 (0), bit 0

Note

To parse bits properly, they must come in multiples of eight.

Bits and Padding#

When generating binary inputs, you may need to adhere to specific lengths. Such lengths are often enforced by padding – that is, adding bits until the required length is achieved. For instance, let us assume you have a field consisting of some bits. However, the overall length of the field must be a multiple of eight to have it byte-aligned. For such padding, define the field as

<field> ::= <bits> <padding>
<padding> ::= 0*

combined with a constraint

where len(<field>) % 8 == 0

Note that applied on derivation trees, len() always returns the number of child elements, not the string length; here, we use this to access the number of elements in <field>.

Contents