Data Converters

When defining a complex input format, some parts may be the result of applying an operation on another, more structured part. Most importantly, content may be encoded, compressed, or converted.

Fandango uses a special form of generators to handle these, called converters. These are generator expressions with symbols, mostly functions that take symbols as arguments. Let’s have a look at how these work.

Encoding Data During Fuzzing

In Fandango, a generator expression can contain symbols (enclosed in <...>) as elements. Such generators are called converters. When fuzzing, converters have the effect of Fandango using the grammar to

• instantiate each symbol from the grammar,

• evaluate the resulting expression, and

• return the resulting value.

Here is a simple example to get you started. The Python base64 module provides methods to encode arbitrary binary data into printable ASCII characters:

import base64

encoded = base64.b64encode(b'Fandango\x01')
encoded

b'RmFuZGFuZ28B'

Of course, these can be decoded again:

base64.b64decode(encoded)

b'Fandango\x01'

Let us make use of these functions. Assume we have a <data> field that contains a number of bytes:

<data> ::= b'Fandango' <byte>+

To encode such a <data> field into an <item>, we can write

<item> ::= rb'.*' := base64.b64encode(bytes(<data>))

This rule brings multiple things together:

• First, we convert <data> into a suitable type (in our case, bytes).

• Then, we invoke base64.b64encode() on it as a generator to obtain a string of bytes.

• We parse the string into an <item>, whose definition is rb'.*' (any sequence of bytes except newline).

In a third step, we embed the <item> into a (binary) string:

<start> ::= b'Data: ' <item>

The full resulting encode.fan spec looks like this:

import base64

<start> ::= b'Data: ' <item>
<item> ::= rb'.*' := base64.b64encode(bytes(<data>))
<data> ::= b'Fandango' <byte>+

With this, we can encode and embed binary data:

$ fandango fuzz -f encode.fan -n 1

Data: RmFuZGFuZ29Nyhg=

In the same vein, one can use functions for compressing data or any other kind of conversion.

Sources, Encoders, and Constraints

When Fandango produces an input using a generator, it saves the generated arguments as a source in the produced derivation tree. Sources become visible as soon as the input is shown as a grammar:

$ fandango fuzz -f encode.fan -n 1 --format=grammar

<start> ::= b'Data: ' <item>  # Position 0x0000 (0); b'Data: RmFuZGFuZ29Nyhg='
  <item> ::= b'RmFuZGFuZ29Nyhg=' := f(<data>)  # Position 0x0006 (6)
    <data> ::= b'Fandango' <byte> <byte> <byte>  # Position 0x0000 (0); b'FandangoM\xca\x18'
      <byte> ::= <_byte>
        <_byte> ::= b'M'  # Position 0x0008 (8)
      <byte> ::= <_byte>
        <_byte> ::= b'\xca'  # Position 0x0009 (9)
      <byte> ::= <_byte>
        <_byte> ::= b'\x18'  # Position 0x000a (10)

In the definition of <item>, we see a generic converter f(<data>) as well as the definition of <data> that went into the generator. (The actual generator code, base64.b64encode(bytes(<data>)), is not saved in the derivation tree.)

We can visualize the resulting tree, using a double arrow between <item> and its source <data>, indicating that their values depend on each other:

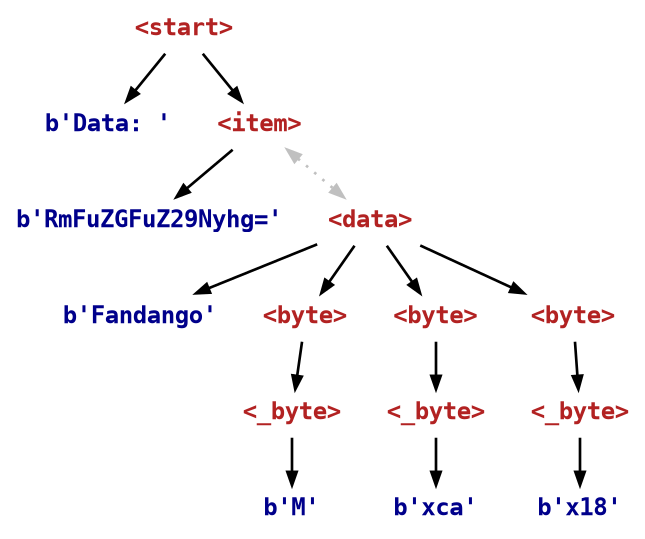
Since sources like <data> are preserved, we can use them in constraints. For instance, we can produce a string with specific values for <data>:

$ fandango fuzz -f encode.fan -n 1 -c '<data> == b"Fandango author"'

Data: RmFuZGFuZ28gYXV0aG9y

Is this string a correct encoding of a correct string? We will see in the next section.

Decoding Parsed Data

So far, we can only encode data during fuzzing. But what if we also want to decode data, say during parsing? Our encode.fan will help us parse the data, but not decode it:

$ echo -n 'Data: RmFuZGFuZ28gYXV0aG9y' | fandango parse -f encode.fan

FandangoValueError: <data>: Missing converter from <item> (<data> ::= ... := f(<item>))
FandangoParseError: 1 error(s) during parsing

The fact that parsing fails is not a big surprise, as we only have specified an encoder, but not a decoder. As the error message suggests, we need to add a generator for <data> - a decoder that converts <item> elements into <data>.

We can achieve this by providing a generator for <data> that builds on <item>:

<data> ::= b'Fandango' <byte>+ := base64.b64decode(bytes(<item>))

Here, base64.b64decode(bytes(<item>)) takes an <item> (which is previously parsed) and decodes it. The decoded result is parsed and placed in <data>.

The resulting encode-decode.fan file now looks like this:

import base64

<start> ::= b'Data: ' <item>
<item> ::= rb'.*' := base64.b64encode(bytes(<data>))
<data> ::= b'Fandango' <byte>+ := base64.b64decode(bytes(<item>))

Fandango allows generators in both directions so one .fan file can be used for fuzzing and parsing.

If this looks like a mutual recursive definition, that is because it is. During fuzzing and parsing, Fandango tracks the dependencies between generators and uses them to decide which generators to use first:

• When fuzzing, Fandango operates top-down, starting with the topmost generator encountered; their arguments are produced. In our case, this is the <item> generator, generating a value for <data>.

• When parsing, Fandango operates bottom-up, starting with the lowest generators encountered; their arguments are parsed. In our case, this is the <data> generator, parsing a value for <item>.

In both case, when Fandango encounters a recursion, it stops evaluating the generator:

• When parsing an <item>, Fandango does not invoke the generator for <data> because <data> is being processed already.

• Likewise, when producing <data>, Fandango does not invoke the generator for <item> because <item> is being processed already.

Let us see if all of this works and if this input is indeed properly parsed and decoded.

$ echo -n 'Data: RmFuZGFuZ28gYXV0aG9y' | fandango parse -f encode-decode.fan -o - --format=grammar

<start> ::= b'Data: ' <item>  # Position 0x0000 (0); b'Data: RmFuZGFuZ28gYXV0aG9y'
  <item> ::= b'RmFuZGFuZ28gYXV0aG9y' := f(<data>)  # Position 0x0006 (6)
    <data> ::= b'Fandango' <byte> <byte> <byte> <byte> <byte> <byte> <byte>  # Position 0x0000 (0); b'Fandango author'
      <byte> ::= <_byte>
        <_byte> ::= b' '  # Position 0x0008 (8)
      <byte> ::= <_byte>
        <_byte> ::= b'a'  # Position 0x0009 (9)
      <byte> ::= <_byte>
        <_byte> ::= b'u'  # Position 0x000a (10)
      <byte> ::= <_byte>
        <_byte> ::= b't'  # Position 0x000b (11)
      <byte> ::= <_byte>
        <_byte> ::= b'h'  # Position 0x000c (12)
      <byte> ::= <_byte>
        <_byte> ::= b'o'  # Position 0x000d (13)
      <byte> ::= <_byte>
        <_byte> ::= b'r'  # Position 0x000e (14)

We see that the <data> element contains the "Fandango author" string we provided as a constraint during generation. This is what the parsed derivation tree looks like:

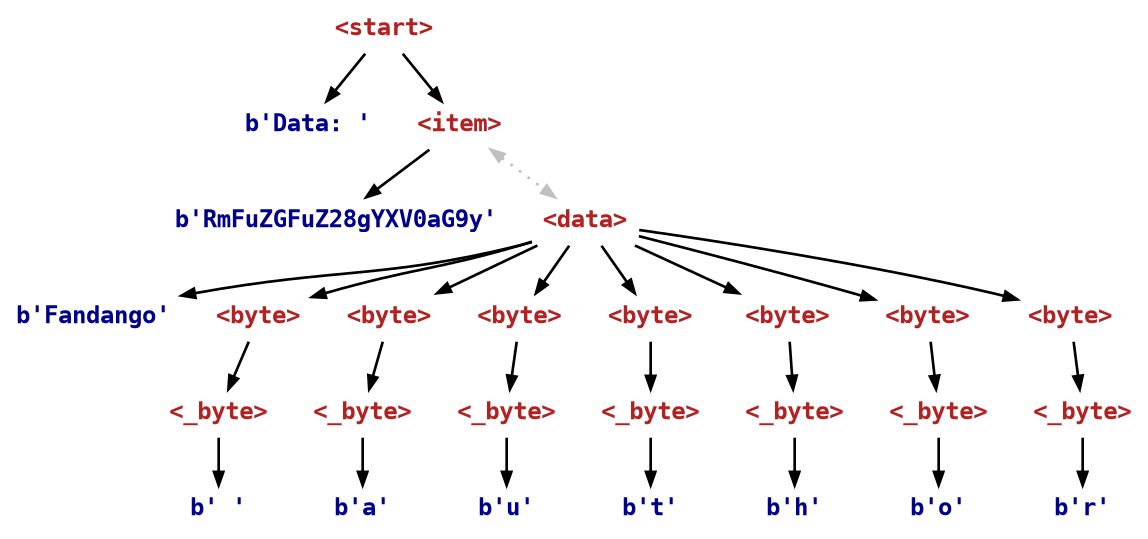
With a constraint, we can check that the decoded string is correct:

$ echo -n 'Data: RmFuZGFuZ28gYXV0aG9y' | fandango parse -f encode-decode.fan -c '<data> == b"Fandango author"'

We get no error - so the parse was successful, and that all constraints hold.

Applications

The above scheme can be used for all kinds of encodings and compressions - and thus allow translations between abstraction layers. Typical applications include:

• Compressed data (e.g. pixels in a GIF or PNG file)

• Encoded data (e.g. binary input as ASCII chars in MIME encodings)

• Converted data (e.g. ASCII to UTF-8 to UTF-16 and back)

Even though parts of the input are encoded (or compressed), you can still use constraints to shape them. And if the encoding or compression can be inverted, you can also use it to parse inputs again.

Converters vs. Constraints

Since converters (and generally, generators) can do anything, they can be used for any purpose, including producing solutions that normally would come from constraints.

As an example, consider the credit card grammar from the chapter on binary inputs:

<start>              ::= <credit_card_number>
<credit_card_number> ::= <number> <check_digit>
<number>             ::= <digit>{15}  # for 16-digit numbers
<check_digit>        ::= <digit>
where <check_digit> == credit_card_check_digit(str(<number>))

Instead of having a constraint (where) that expresses the relationship between <number> and <check_digit>, we can easily enhance the grammar with converters between <number> and <credit_card_number>:

<credit_card_number> ::= <number> <check_digit> := add_check_digit(str(<number>))
<number>             ::= <digit>{15} := strip_check_digit(str(<credit_card_number>))

with

def add_check_digit(number: str) -> str:
    """Add a check digit to the credit card number `number`."""
    check_digit = credit_card_check_digit(number)
    return number + check_digit

and

def strip_check_digit(number: str) -> str:
    """Strip the check digit from the credit card number `number`."""
    return number[:-1]

The resulting .fan spec credit_card-gen.fan has the same effect as the original credit_card.fan from the chapter on binary inputs:

$ fandango fuzz -f credit_card-gen.fan -n 10

0914130799284054
8989412847017394
2830912617222177
1393638740755848
2425149970124424
5911864378071183
2631029393759701
2845061574728546
6079440611328379
6874893687279370

Now, these two functions add_check_digit() and strip_check_digit() are definitely longer than our original constraint

where <check_digit> == credit_card_check_digit(str(<number>))

However, they are not necessarily more complex. And they are more efficient, as they provide a solution right away. So when should one use constraints, and when converters?

Tip

In general:

• If you have a simple, operational way to solve a problem, consider a converter.

• If you want a simple, declarative way to specify your needs, use a constraint.